syren-halofit: A fast, interpretable, high-precision formula for the LCDM nonlinear matter power spectrum

Download paper here

Abstract

Context: Rapid and accurate evaluation of the nonlinear matter power spectrum, $P(k)$, as a function of cosmological parameters and redshift is of fundamental importance in cosmology. Analytic approximations provide an interpretable solution, yet current approximations are neither fast nor accurate relative to black-box numerical emulators.

Aims: To accelerate symbolic approximations to $P(k)$ by removing the requirement to perform integrals, instead using short symbolic expressions to compute all variables of interest. We also wish to make such expressions more accurate by re-optimising the parameters of these models (using a larger number of cosmologies and focusing on cosmological parameters of more interest for present-day studies) and providing correction terms.

Methods: We use symbolic regression to obtain simple analytic approximations to the nonlinear scale, $k_\sigma$, the effective spectral index, $n_{\rm eff}$, and the curvature, $C$, which are required for the halofit model. We then re-optimise the coefficients of halofit to fit a wide range of cosmologies and redshifts. We then again exploit symbolic regression to explore the space of analytic expressions to fit the residuals between $P(k)$ and the optimised predictions of halofit. All methods are validated against $N$-body simulations.

Results: We find symbolic expressions for $k_\sigma$, $n_{\rm eff}$ and $C$ which have root mean squared fractional errors of 0.8%, 0.2% and 0.3%, respectively, for redshifts below 3 and a wide range of cosmologies. We provide re-optimised halofit parameters, which reduce the root mean squared fractional error from 3% to below 2% for wavenumbers $k=9\times10^{-3}-9 \, h{\rm Mpc^{-1}}$. We introduce syren-halofit (symbolic-regression-enhanced halofit), an extension to halofit containing a short symbolic correction which improves this error to 1%. Our method is 2350 and 3170 times faster than current halofit and hmcode implementations, respectively, and 2680 and 64 times faster than EuclidEmulator (which requires running class) and the BACCO emulator. We obtain comparable accuracy to EuclidEmulator and the BACCO emulator when tested on $N$-body simulations.

Conclusions: Our work greatly increases the speed and accuracy of symbolic approximations to $P(k)$, making them significantly faster than their numerical counterparts without loss of accuracy.

Code

Python and fortran functions with the analytic emulators can be accessed here.

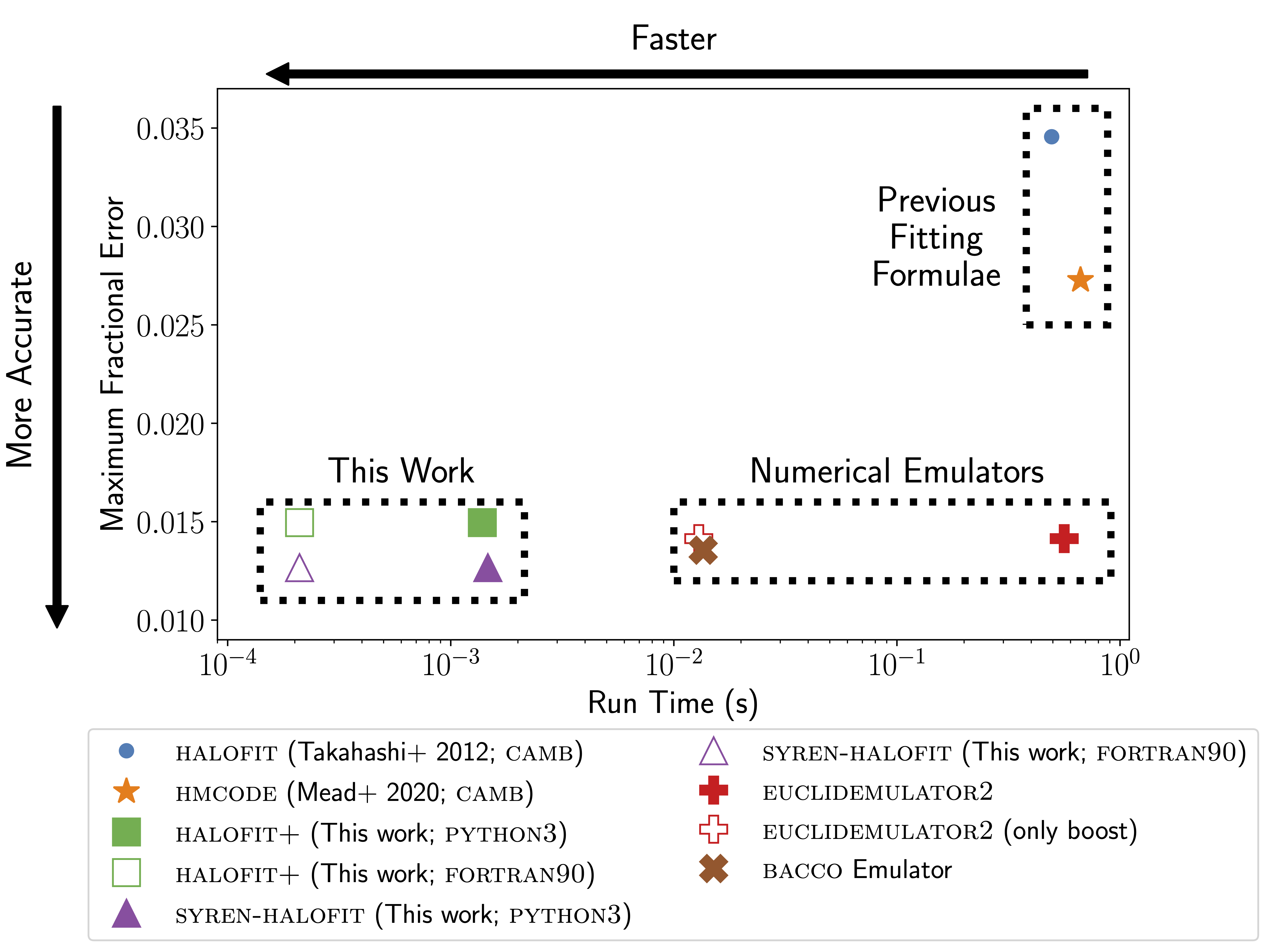Maximum (between $z=0$ and $1$) root mean squared fractional error with respect to the Quijote power spectra against run time for various nonlinear power spectrum emulators. The run time of EuclidEmulator2 is dominated by the Boltzmann code class; the emulation run time is comparable to that of the BACCO emulator, as indicated by the unfilled cross. Our results are orders of magnitude faster than the other methods, with our best method – syren-halofit – achieving even greater accuracy than the numerical emulators.