Background

Dark matter makes up ~25% of the universe’s mass and is the key component in structure formation. Our knowledge of dark matter currently comes solely from its gravitational influence, but revealing its particle nature will require identifying its other interaction with itself and standard model particles. Fig 1 shows the three processes that such interactions would allow: production of dark matter through collision of standard model particles, scattering between dark matter and standard model particles, and annilihation of dark matter into standard matter particles. Each of these has an associated detection method: we could produce dark matter in particle colliders (“direct detection”), see recoils of standard model particles due to incident dark matter (“scattering”), or identify standard model particles produced by dark matter annihilations (“indirect detection”). A final possible interaction, included in “indirect detection” but involving only a single dark matter particle, is the spontaneous decay of dark matter into standard model particles.

Cartoon illustrating the ways in which dark matter may interact with Standard Model particles.

We are concerned here with dark matter annihilation and decay. This is typically sought by identifying astrophysical objects whose kinematics indicate that they are particularly dark matter-rich, which include the Milky Way, dwarf spheroidal galaxies (dSphs) in the Local Group and massive clusters further afield. One then targets these objects with telescopes sensitive to gamma-rays, which the standard model particles produced by dark matter would be expected to decay into. These searches have enabled us to rule out a thermal relic origin for WIMP dark matter at low mass, depending on the annihilation channel. Such methods however have two important disadvantages:

1. by focusing on specific objects they necessarily miss gamma-rays coming from the interactions of any dark matter not in the objects,
2. they are susceptible to systematic errors due to gamma-rays produced in those objects by non-dark matter, i.e. baryonic, means.

To avoid these potential pitfalls, we instead forward-model the gamma-ray flux from annihilation and decay pixel-by-pixel across the full sky using BORG-based models of the large-scale dark matter distribution. This enables a field-level inference of annihilation and decay rates on comparison with similarly all-sky data from the Fermi Large Area Telescope.¹

Predicting annihilation and decay fluxes

Our method leverages CSiBORG, a suite of 101 high-resolution N-body simulations with initial conditions spanning the posterior of the 2M++ BORG-PM chain. Each box provides a plausible realisation of the dark matter distribution out to ~200 Mpc, including the clumping of dark matter into halos. We use this to make a prediction for the annihilation (decay) flux that would be seen for each line of sight on the sky for a given annihilation cross-section (decay rate) and channel, which we then project onto a Healpix grid to match the resolution of Fermi. This is shown in Fig 2, in terms of the “J-factor” (left) and “D-factor” (right) that describe the astrophysical contributions to the flux (i.e. without the particle physics terms). Assuming a Poisson likelihood for the measured flux in each pixel, and marginalising over the CSiBORG realisations, a model for substructure within each halo and a set of templates that describes the contribution from non-dark matter sources, we constrain the parameters of dark matter interactions using all nearby dark matter that is resolved by CSiBORG.

Full-sky Mollweide projection in galactic coordinates of the ensemble mean J and D factors over the CSiBORG realisations. These are proportional to the gamma-ray flux produced by dark matter annihilation and decay respectively.

Bounding DM interactions

We find no evidence for enhanced gamma-ray flux tracing dark matter density squared, as would be expected in an annihilation model. This allows us to set constraints on the cross-section, which we show in Fig 3 (left) as a function of dark matter particle mass for a range of different annihilation channels. The grey dot-dashed line shows the thermal relic cross-section, which is the value needed to explain the current dark matter abundance through thermal freeze-out in the early universe (the standard production mechanism for WIMPs). Locations where bounds are below this indicate that the thermal relic scenario is ruled out. The black dashed line shows a previous constraint from cross-correlation of gamma-ray flux with the positions of low surface brightness galaxies, and the dotted line is from dSphs in the Local Group. While these constraints are much stronger than ours as dSphs are very close leading to large predicted flux (not included in our analysis because they are below the CSiBORG resolution limit), they are sensitive to flux contributions from baryonic processes. In our approach, significant constraining power comes from regions largely devoid of baryons such as the filaments that connect halos.

The right panel of Fig 3 shows our constraint on the flux due to dark matter decays, separately for each of Fermi’s energy bins. That many are centred away from zero indicates that we do detect gamma-rays with a flux distribution across the sky that traces the dark matter density, as expected for decays. However, the spectrum of the signal is much more closely aligned with a power-law than the expectation from decay (pink vs red line), suggesting a more mundane, baryonic origin such as blazars.

In conclusion, we have used BORG to open yet another field – dark matter indirect detection – to full-sky, field-level Bayesian inference. In principle this allows all the information to be extracted from gamma-ray surveys and thus represents the most promising astrophysical method for uncovering the non-gravitational interactions of dark matter.

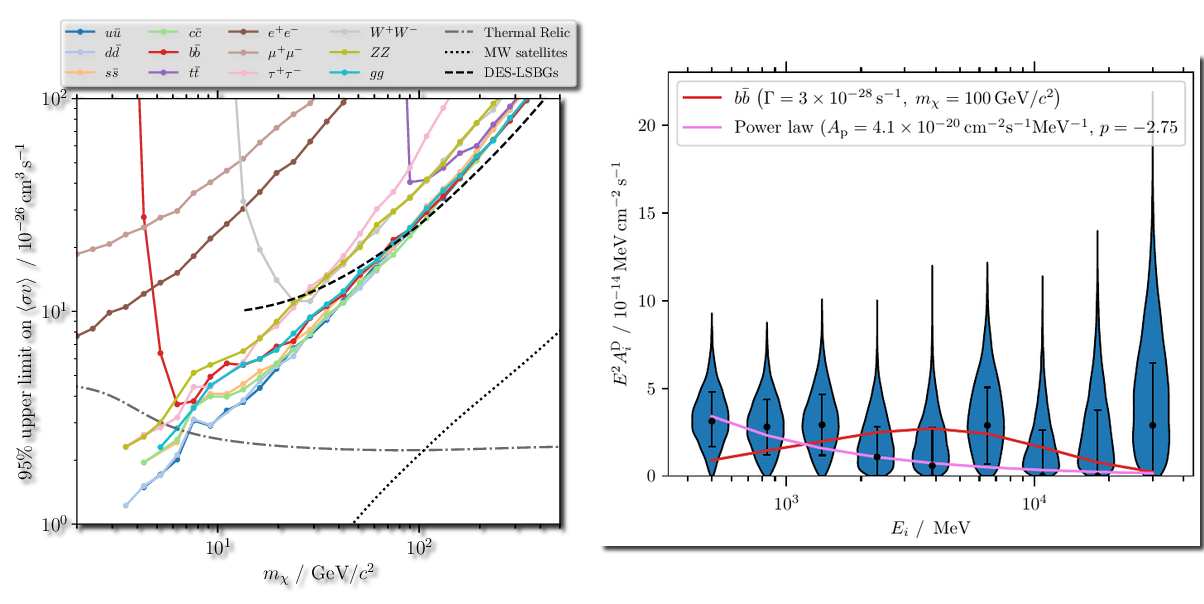Left: 2\(\sigma\) bounds on the dark matter annihilation cross-section for various different channels (coloured lines). The grey dot-dashed line is the cross-section of a thermal relic WIMP, and the black dashed and dotted lines show literature constraints from galaxy cross-correlations and Local Group dwarf spheroidals respectively. Right: Flux contribution with the spatial distribution expected from dark matter decay in each Fermi energy bin. The red line is the spectrum expected from decays to \(b\bar{b}\), while the pink line, preferred by the data, is the best-fit power-law spectrum.

Overview

A fundamental assumption in our current theories of the Universe is that photons always travel at the same speed, \(c\), independent of their energy. But this needs not be true. If the photon had a non-zero rest mass, then lower energy photons would travel slower (\(v < c\)). Alternatively, it is expected that quantum fluctuations of spacetime at high energies in so-called quantum gravity (QG) theories would make spacetime appear “foamy”, and thus empty space would have an energy-dependent refractive index. Or perhaps photons of different energy couple to gravity with different strengths (and thus violate the weak equivalence principle), so that photons of different energy travel differently through a gravitational field. In any one of these cases, photons of different energies from a distant source would arrive at different times, even if they were emitted simultaneously. Since the expected time delay increases with distance travelled, by studying the energy-dependent arrival times (spectral lag) of photons from sources at high redshift, we can place tight constraints on the quantum gravity length scale, \(\ell_{\rm QG}\), the photon mass, \(m_\gamma\), or the different couplings of photons to gravity at different energy, \(\Delta \gamma\). The high redshifts and short durations of Gamma Ray Bursts (GRBs) are ideal for this, so this is what we consider here. For the majority of Gamma Ray Burts, high energy photons are detected before lower energy photons, which is qualitatively the same as for a massive photon and some quantum gravity models, and could thus provide evidence for such theories.

The gravitational time delay

To constrain the equivalence principle, we must be able to predict how long it takes a photon to travel through a gravitational field. The resulting time delay to a distant source depends on the gravitational potential along the path that it travels and thus depends on the direction in the sky. If one had knowledge of the true present-day matter field, then one could create maps of the expected time delay as a function of source position. Indeed, in previous attempts to constrain equivalence-principle violation, \(\delta \phi\) was modelled as arising from one or a few isolated sources near the line of sight, however the long range of gravity casts doubt on the multiple point masses approximation. Instead, we account fully for the contributions to the time delay from all mass in the non-linear cosmological density field. We derive the contribution from local structures using constrained density fields generated by the BORG reconstruction of SDSS-III/BOSS ¹, and combine this with an unconstrained contribution from distant sources to produce a Monte-Carlo based source-by-source forward model for the expected time delay. The ensemble mean of the resulting time delay fluctuation map is plotted in Figure 1, and is \(\sim 10^{11} {\rm \, s}\) for a source at \(z=0.1\).

Mollweide projection in equatorial coordinates of the ensemble mean of the time delay fluctuations at \(z=0.1\) from wavelengths resolved by the BORG reconstruction.

Forward modelling the time delays

We use a catalogue of 668 Gamma Ray Bursts for the BATSE satellite since these not only have spectral lag data, but also pseudoredshifts calculated using the spectral peak energy-peak luminosity relation. Propagating uncertainties on the pseudoredshifts, sky localisation and spectral parameters through Monte Carlo Sampling, we produce source-by-source forward models for the likelihood of a time delay from quantum gravity, a photon mass or equivalence principle violation. However, these are not the only types of physics that can lead to spectral lags: these may also be generated through intrinsic differences in the emission of photons of different wavelength at the source or their propagation through the medium surrounding the Gamma Ray Burst, or through instrumental effects at the observer. Without a robust physical model for the time delays these lead to, we model them using a generic functional form (a sum of Gaussians) with free parameters that we marginalise over in constraining \(m_\gamma\), \(\ell_{QG}\) and \(\Delta\gamma\). We vary the number of Gaussians used to describe these observational and astrophysical processes to find the best-fitting model to the data. Importantly, we find that our results are insensitive to this choice; a vital check that was often neglected in previous work. We compare our predicted time delays to the observed ones through a MCMC algorithm and therefore constrain \(m_\gamma\), \(\ell_{QG}\) and \(\Delta\gamma\).

Is the speed of light energy dependent?

We find no evidence that the speed of light has an energy dependence. We constrain the photon mass to be \(m_\gamma < 4.0 \times 10^{-5} \, h \, {\rm eV}/c^2\) and the quantum gravity length scale to be \(\ell_{\rm QG} < 5.3 \times 10^{-18} \, h \, {\rm \, GeV^{-1}}\) at 95% confidence ². As shown in Figure 2, the quantum gravity constraint is the tightest from time delay studies which consider multiple Gamma Ray Bursts, and the constraint on \(m_\gamma\), although weaker than from using radio data, provides an independent constraint which is less sensitive to the effects of dispersion by electrons. We also place upper limits on an energy dependence of \(\gamma\) of \(\Delta \gamma < 2.1 \times 10^{-15}\) at \(1 \sigma\) confidence between photon energies of \(25 {\rm \, keV}\) and \(325 {\rm \, keV}\) ³. These constraints are 40 times tighter than literature results, illustrating the benefits of using complete mass distributions when studying non-local relativistic effects such as time delays.

So what can we say about quantum gravity, the photon mass and the equivalence principle? Through the use of simulation based, Bayesian statistical forward-modelling techniques and the BORG algorithm, we have produced some of the tightest constraints on these theories to date, and have demonstrated that the results are robust to how one models other astrophysical and observational contributions to the observed signal. It is expected that \(\ell_{\rm QG}\) should be near the Planck length, which is approximately two orders of magnitude smaller than we are currently sensitive to, so we are yet to probe this. It is expected that detecting Gamma Ray Bursts at \(>100 {\rm \, GeV}\) should be routine in the future; with more, higher energy measurements one should begin to probe this energy scale, so there is the tantalising possibility of making the first detection of quantum gravity as these limits approach the Planck scale in the near future.

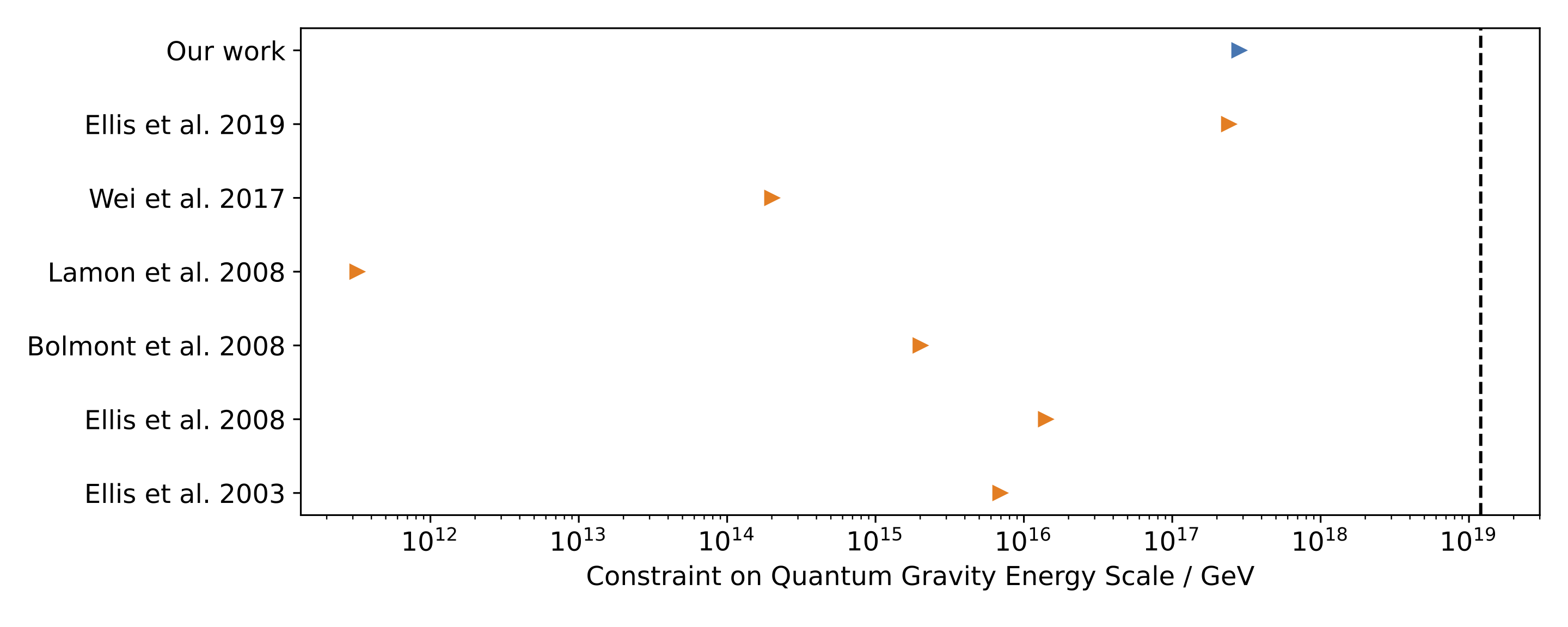Lower limits on the quantum gravity energy scale (\(1 / \ell_{\rm QG}\)) from time delay studies which use multiple astrophysical sources. Our work provides the tightest constraint to date. The dashed vertical line is the Planck energy, and it is expected that the quantum gravity energy scale has approximately this value.