A precise symbolic emulator of the linear matter power spectrum

Download paper here

Abstract

Context: Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used.

Aims: To construct an efficient, differentiable, interpretable, symbolic emulator for the redshift zero linear matter power spectrum which achieves sub-percent level accuracy. We also wish to obtain a simple analytic expression to convert $A_{\rm s}$ to $\sigma_8$ given the other cosmological parameters.

Methods: We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation.

Results: We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred.

Conclusions: It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.

Code

Python functions with the analytic emulators can be accessed here.

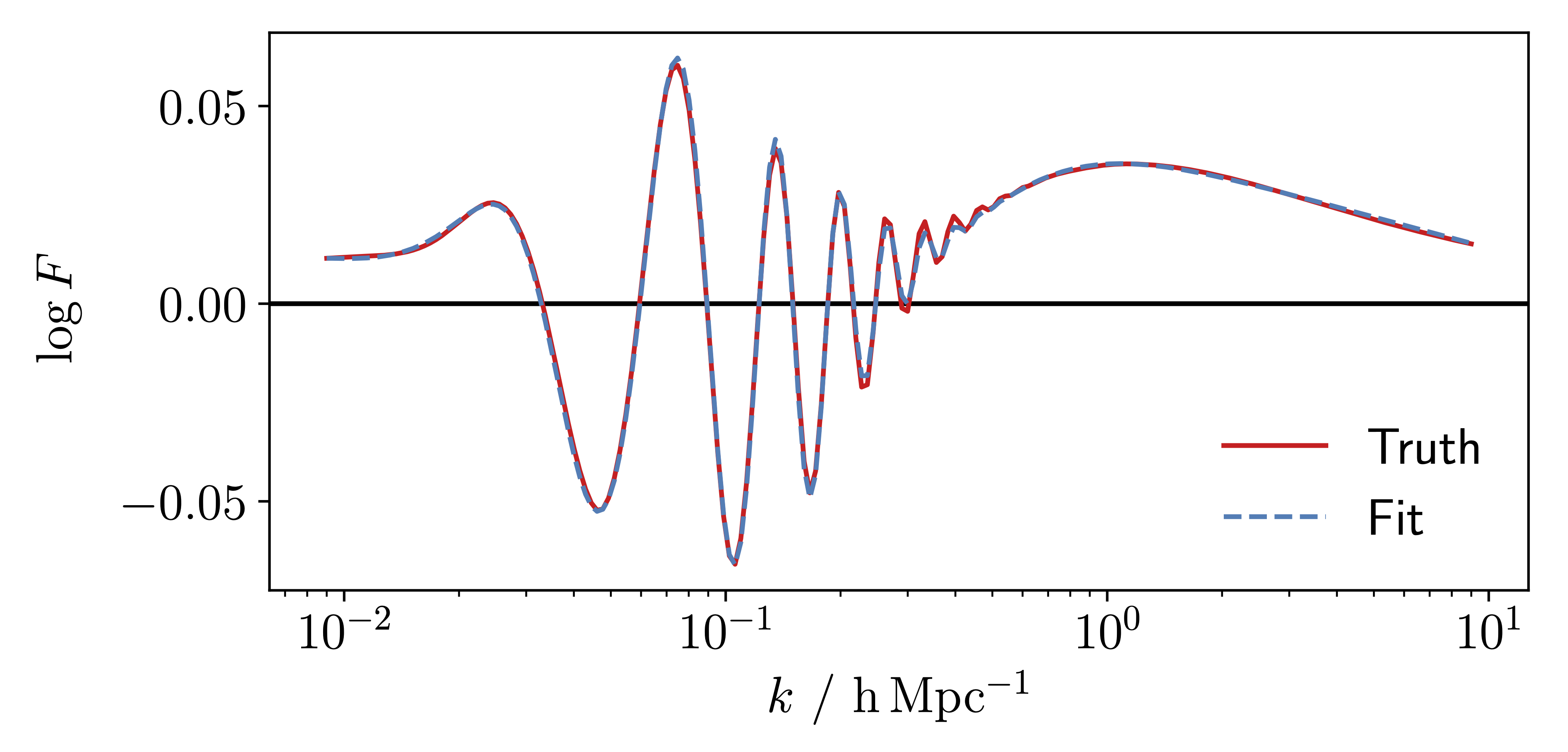Residuals between the linear matter power spectrum and the Eisenstein & Hu fit without baryons for the Planck 2018 cosmology. We plot the truth computed with CAMB with solid red lines, and the analytic fit obtained in this paper with dashed blue lines. We see that the fit is accurate within 0.3% across all $k$ considered.