Symbolic Regression and Differentiable Fits in Beyond the Standard Model Physics

Download paper here

Abstract

We demonstrate the efficacy of symbolic regression (SR) to probe models of particle physics Beyond the Standard Model (BSM), by considering the so-called Constrained Minimal Supersymmetric Standard Model (CMSSM). Like many incarnations of BSM physics this model has a number (four) of arbitrary parameters, which determine the experimental signals, and cosmological observables such as the dark matter relic density. We show that analysis of the phenomenology can be greatly accelerated by using symbolic expressions derived for the observables in terms of the input parameters. Here we focus on the Higgs mass, the cold dark matter relic density, and the contribution to the anomalous magnetic moment of the muon. We find that SR can produce remarkably accurate expressions. Using them we make global fits to derive the posterior probability densities of the CMSSM input parameters which are in good agreement with those performed using conventional methods. Moreover, we demonstrate a major advantage of SR which is the ability to make fits using differentiable methods rather than sampling methods. We also compare the method with neural network (NN) regression. SR produces more globally robust results, while NNs require data that is focussed on the promising regions in order to be equally performant.

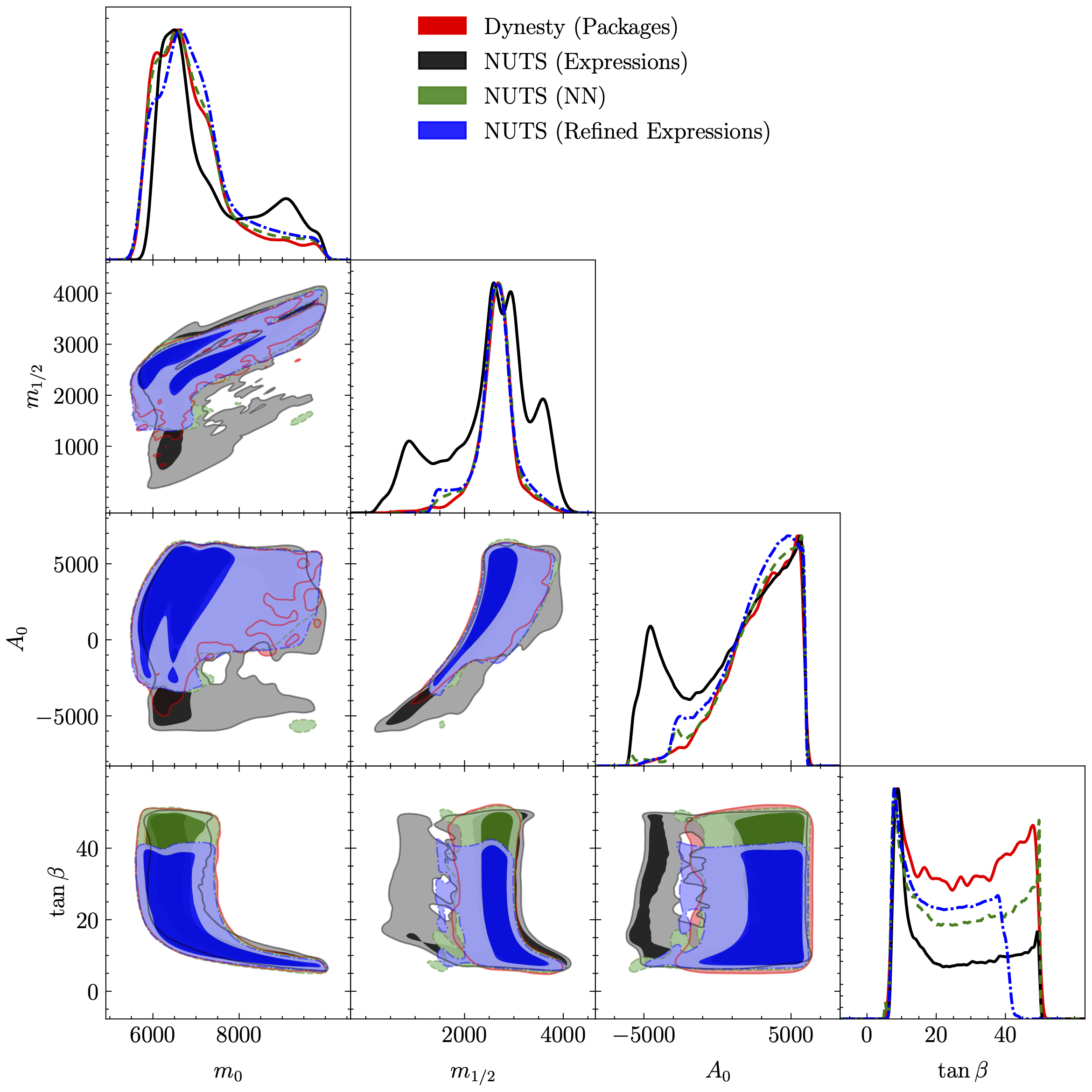Posterior distribution of CMSSM parameters obtained using NUTS compared to those from Dynesty. The contours show the 68% and 95% confidence intervals. The red contours compute the outputs exactly, whereas the remaining ones use the expressions of Ref. 27 (black), a neural network (green), or refined symbolic expressions for a narrower prior range (blue) to bypass this calculation. The 1D marginals are normalized with respect to their maximum heights rather than areas in order to assess the agreement of maximum a posteriori probabilities.