syren-new: Precise formulae for the linear and nonlinear matter power spectra with massive neutrinos and dynamical dark energy

Download paper here

Abstract

Context: Current and future large scale structure surveys aim to constrain the neutrino mass and the equation of state of dark energy. To do this efficiently, rapid yet accurate evaluation of the matter power spectrum in the presence of these effects is essential.

Aims: We aim to construct accurate and interpretable symbolic approximations to the linear and nonlinear matter power spectra as a function of cosmological parameters in extended $\Lambda$CDM models which contain massive neutrinos and non-constant equations of state for dark energy. This constitutes an extension of the syren-halofit emulators to incorporate these two effects, which we call syren-new (SYmbolic-Regression-ENhanced power spectrum emulator with NEutrinos and $W_0-w_a$). We also wish to obtain a simple approximation to the derived parameter $\sigma_8$ as a function of the cosmological parameters for these models.

Methods: We utilise symbolic regression to efficiently search through candidate analytic expressions to approximate the various quantities of interest. Our results for the linear power spectrum are designed to emulate CLASS, whereas for the nonlinear case we aim to match the results of EuclidEmulator2. We compare our results to existing emulators and $N$-body simulations.

Results: Our analytic emulators for $\sigma_8$, the linear and nonlinear power spectra achieve root mean squared errors of 0.1%, 0.3% and 1.3%, respectively, across a wide range of cosmological parameters, redshifts and wavenumbers. The error on the nonlinear power spectrum is reduced by approximately a factor of 2 when considering observationally plausible dark energy models and neutrino masses. We verify that emulator-related discrepancies are subdominant compared to observational errors and other modelling uncertainties when computing shear power spectra for LSST-like surveys. Our expressions have similar accuracy to existing (numerical) emulators, but are at least an order of magnitude faster, both on a CPU and GPU.

Conclusions: Our work greatly improves the accuracy, speed and range of applicability of current symbolic approximations to the linear and nonlinear matter power spectra. These now cover the same range of cosmological models as many numerical emulators with similar accuracy, but are much faster and more interpretable. We provide publicly available code for all symbolic approximations found.

Code

Implementations of the analytic emulators can be accessed here.

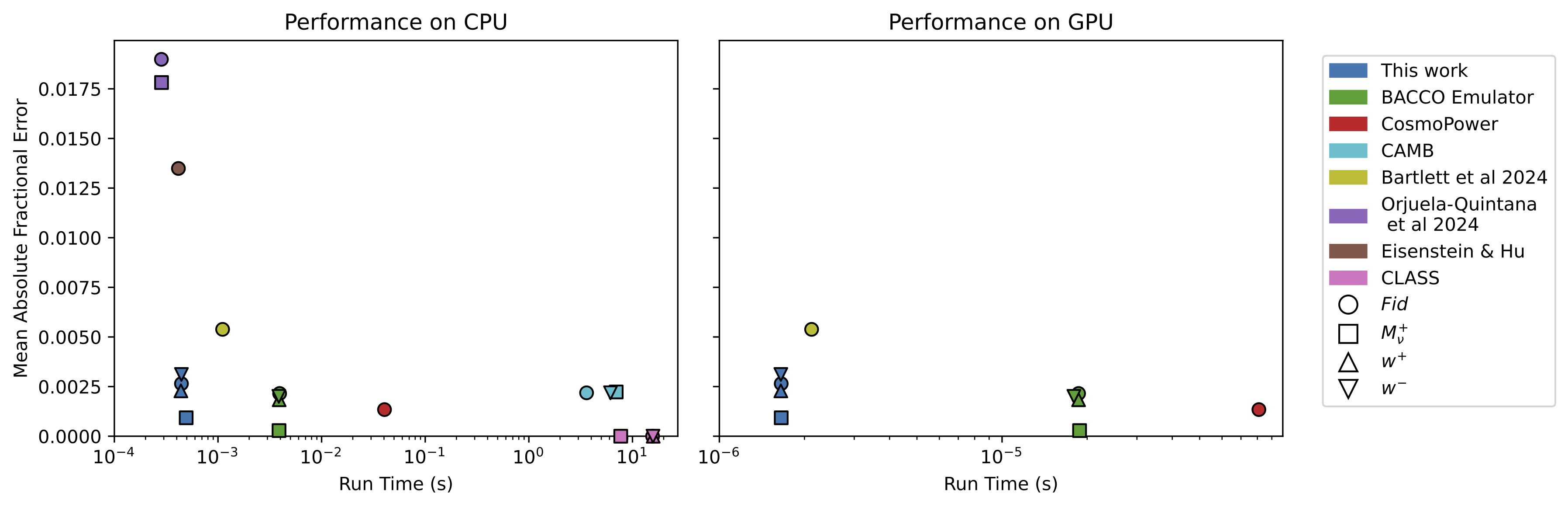Mean absolute fractional error (averaged over 200 logarithmically spaced $k \in [ 9 \times 10^{-3}, 9 ] \, h \, \text{Mpc}^{-1}$) with respect to CLASS against run time for various linear power spectrum emulators at four cosmologies and redshift 0. Some emulators are tested on both CPU (left panel) and GPU (right panel). The different colours refer to the emulator used, whereas each cosmology (defined in Section 7.1) is denoted by a different symbol. Our expressions have similar accuracy to existing (numerical) emulators, but are at least an order of magnitude faster, both on a CPU and GPU.