Marginalised Normal Regression: Unbiased curve fitting in the presence of x-errors

Download paper here

Abstract

The history of the seemingly simple problem of straight line fitting in the presence of both $x$ and $y$ errors has been fraught with misadventure, with statistically ad hoc and poorly tested methods abounding in the literature. The problem stems from the emergence of latent variables describing the “true” values of the independent variables, the priors on which have a significant impact on the regression result. By analytic calculation of maximum a posteriori values and biases, and comprehensive numerical mock tests, we assess the quality of possible priors. In the presence of intrinsic scatter, the only prior that we find to give reliably unbiased results in general is a mixture of one or more Gaussians with means and variances determined as part of the inference. We find that a single Gaussian is typically sufficient and dub this model Marginalised Normal Regression (MNR). We illustrate the necessity for MNR by comparing it to alternative methods on an important linear relation in cosmology, and extend it to nonlinear regression and an arbitrary covariance matrix linking $x$ and $y$. We publicly release a Python/Jax implementation of MNR and its Gaussian mixture model extension that is coupled to Hamiltonian Monte Carlo for efficient sampling, which we call roxy (Regression and Optimisation with X and Y errors).

Code

The roxy code is available here.

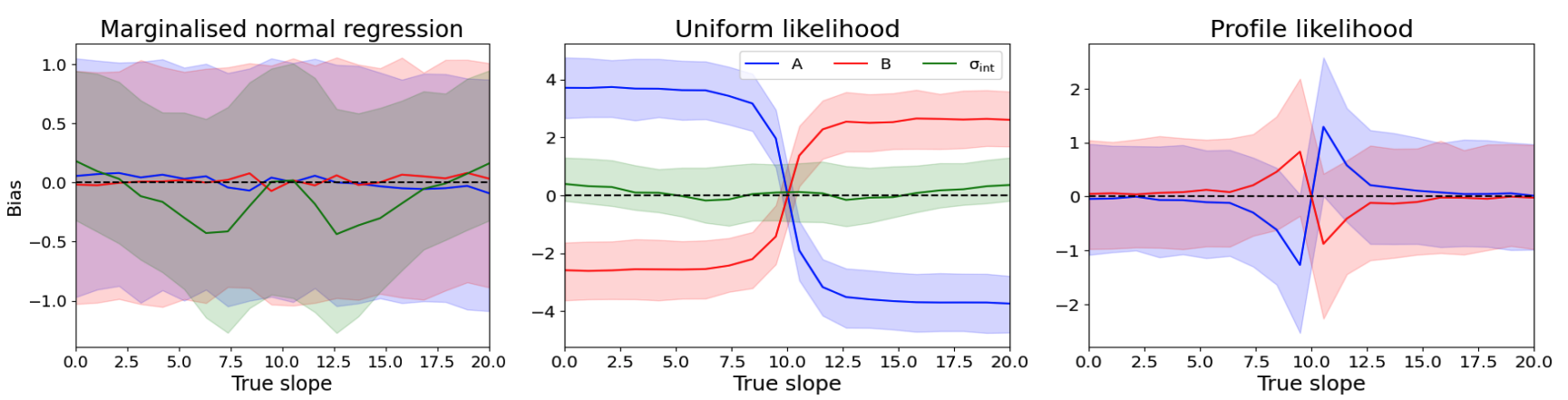Distribution of biases incurred by the MNR (left), unif (centre) and prof (right) methods in the slope (blue), intercept (red) and intrinsic scatter (green) of the straight line as the slope is varied with the other parameters held at their fiducial values (see Table 1). While the unif and prof methods are often wildly biased, mnr has a sub-1$\sigma$ average bias in all cases, with the bias distribution typically conforming very closely to the expected standard normal.